Bu çalışmada ele alacağımız zaman serisi modelleri tek değişkenlidir ve kendi geçmiş değerleri ve hatalarına (kalıntılar) göre kurulan modellerdir.
\(Y_t\) gibi bir serimiz olsun. Bu durumda sözel olarak ifade edilen şey aşağıdaki gibi olur:
\(Y_t = f(Y_{t-1},Y_{t-2}, ...,\epsilon_t,\epsilon_{t-1},\epsilon_{t-2},...)\)
Otoregresif Süreç: AR(p)
AR modeller, bir zaman serisinin herhangi bir dönemdeki gözlem değerini, aynı serinin ondan önceki belirli sayıda dönemin gözlem değerinin ve hata teriminin doğrusal bir bileşimi olarak ifade eden modellerdir.
AR(p) süreci şöyle ifade edilir:
\(Y_t = \delta + \phi_1Y_{t-1} + \phi_2Y_{t-2} + ... + \phi_pY_{t-p} + \epsilon_t\)
p = 1 olduğunu varsayalım. Bu, AR(1) sürecidir. Buna aynı zamanda birinci derece otoregresif zaman serisi modeli de diyebiliriz. Çünkü, \(Y_t\) sadece kendi bir önceki dönemi olan \(Y_{t-1}\)’e ve bir rassal kalıntı olan \(\epsilon_t\)’ye bağlıdır.
\(Y_t = \delta + \phi_1Y_{t-1} + \epsilon_t; t = 1,2,...,T\)
\(\delta:\) Sabit parametre (\(Y_t\)’nin ortalaması),
\(\phi_1:\) -1 ile 1 arasında değer aldığı varsayılan bilinmeyen parametre,
\(\epsilon_t:\) Ortalaması sıfır ve sabit varyanslı \(\sigma_{\epsilon}^2\) korelasyonsuz bir hata terimidir: \(\epsilon_t \sim IID (0,\sigma^2)\)
AR(1) süreci için simülasyon ile alternatif yapılar oluşturalım.
\(\phi_1 = 0\) için \(Y_t = \epsilon_t\) olur.
\(\phi_1 = 0.3\) için \(Y_t = 0.3Y_{t-1} + \epsilon_t\) olur.
\(\phi_1 = 0.5\) için \(Y_t = 0.5Y_{t-1} + \epsilon_t\) olur.
\(\phi_1 = 0.7\) için \(Y_t = 0.7Y_{t-1} + \epsilon_t\) olur.
\(\phi_1 = 0.9\) için \(Y_t = 0.9Y_{t-1} + \epsilon_t\) olur.

Yukarıda, ilk simüle ettiğimiz \(\phi_{1} = 0\)’ın çok sık bir biçimde ortalamayı kestiğini ve \(\phi_1\)’in değeri arttıkça ortalamayı daha az kestiğini görüyoruz. \(\phi_1\) için -1 ile 1 arasında değer aldığı varsayılan bilinmeyen parametre demiştik. Yani, -1 < \(\phi_1\) < 1 ya da \(|\phi_1| < 1\) şeklinde de yazabiliriz. Eğer \(\phi_1 = 1\) olursa ki bu grafikte yok; sürecin durağan olmadığı yorumunu yapabiliriz.
Hareketli Ortalama Süreci: MA(q)
MA modeller, bir zaman serisinin herhangi bir dönemindeki gözlem değerinin, aynı döneminin hata terimi ve belirli sayıda geçmiş dönemin hata terimlerinin doğrusal bir bileşimi olarak ifade edildiği modellerdir.
MA(q) süreci şöyle ifade edilir:
\(Y_t = \mu + \epsilon_t + \theta_1\epsilon_{t-1} + \theta_2\epsilon_{t-2} + ... + \theta_q\epsilon_{t-q}\)
q = 1 olduğunu varsayalım. Bu, MA(1) sürecidir. Buna aynı zamanda birinci derece hareketli ortalama süreci de diyebiliriz. MA(1) sürecini şöyle ifade edebiliriz:
\(Y_t = \mu + \epsilon_t + \theta_1\epsilon_{t-1}\)
Finans üzerinden örneklendirelim. t günündeki hisse senedinin fiyatı \(P_t\) olsun. Bu durumda bir günden diğerine fiyattaki değişmeyi şöyle ifade edebiliriz: \(Y_t = P_t - P_{t-1} = \epsilon_t; t = 1,2,...,T\)
Beklenmeyen haberlerin olduğu bir ortamda etkisi bir gün içinde geçmeyebilir. Yani, fiyat değişmeleri sonraki günlerde de etkilenebilir. Örneğin, \(Y_{t+1} = \epsilon_{t+1} + \theta_1\epsilon_t\) olabilir. Burada, \(\epsilon_{t+1}\), t+1 günündeki alınan yeni haberlerin/bilgilerin etkisini gösterir. \(\theta_1\epsilon_t\) ise bir gün öncesinin haber etkisinin devamıdır. Şunu diyebiliriz: \(Y_{t+1}\)’in değeri cari ve geçmiş rassal bir kalıntının ağırlıklı ortalamasıdır.
MA sürecinde \(Y_t\)’nin k sayıda gecikmesi ile olan kovaryansı sıfırdır. Yani, \(Cov(Y_t,Y_{t-k}) = \gamma_k = 0\)’dır. Örneğin, MA(1) sürecinde k > 1 olduğu bütün durumlarda kovaryanslar sıfırdır. Bu da MA(1) sürecinin yalnızca bir dönemlik bir belleğe sahip olduğunu ifade eder. Yani, \(Y_t\), sadece \(Y_{t-1}\) ve \(Y_{t+1}\) ile korelasyonludur, diğer gecikmelerle arasında herhangi bir korelasyon yoktur.
MA(1) süreci için simülasyon ile alternatif yapılar oluşturalım.
\(\theta_1 = 0\) için \(Y_t = \epsilon_t\) olur.
\(\theta_1 = -0.3\) için \(Y_t = \epsilon_t - 0.3\epsilon_{t-1}\) olur.
\(\theta_1 = -0.5\) için \(Y_t = \epsilon_t - 0.5\epsilon_{t-1}\) olur.
\(\theta_1 = -0.7\) için \(Y_t = \epsilon_t - 0.7\epsilon_{t-1}\) olur.
\(\theta_1 = -0.9\) için \(Y_t = \epsilon_t - 0.9\epsilon_{t-1}\) olur.

AR(1) sürecindeki simülasyondan farklı olarak MA(1) sürecinde \(\phi_1\) değerleri değiştikçe ortalamayı kesme sıklığında bir değişiklik görülmemektedir.
Otoregresif Hareketli Ortalama Süreci: ARMA(p,q)
Bazen bir zaman serisi hem AR hem de MA sürecini içerebilir. Bu modellerde bir zaman serisinin herhangi bir dönemine ait gözlem değeri, ondan önceki belirli sayıda gözlem değerinin ve hata teriminin doğrusal bir bileşimi olarak ifade edilir.
\(Y_t = \delta + \phi_1Y_{t-1} + \phi_2Y_{t-2} + ... + \phi_pY_{t-p} + \epsilon_t + \mu + \epsilon_t + \theta_1\epsilon_{t-1} + \theta_2\epsilon_{t-2} + ... + \theta_q\epsilon_{t-q}\)
Kesme terimi \(\delta\), \(Y_t\)’nin ortalamasıdır. \(\epsilon_t\) hatalar, \(E(\epsilon_t) = 0\) ve \(Var(\epsilon_t) = \sigma_\epsilon^2\) ile korelasyonsuz rassal değişkenlerdir. Süreç durağan ise ki bunun koşulu aşağıdadır, tüm dönemler için sabir bir ortalama, \(\mu\), söz konusudur.
Durağanlık koşulu: \(\phi_1 + \phi_2 + ... + \phi_p < 1\)’dir.
p = 1 ve q = 1 olsun. Bu bir ARMA(1,1) sürecidir.
\(Y_t = \delta + \phi_1Y_{t-1} + \epsilon_t + \theta_1\epsilon_{t-1}\)
ARMA(1,1) süreci için simülasyon ile alternatif yapılar oluşturalım.
\(\phi_1 = 0.3\) ve \(\theta_1 = -0.3\) için \(Y_t = 0.3Y_{t-1} + \epsilon_t - 0.3\epsilon_{t-1}\) olur.
\(\phi_1 = 0.8\) ve \(\theta_1 = -0.3\) için \(Y_t = 0.8Y_{t-1} + \epsilon_t - 0.3\epsilon_{t-1}\) olur.
\(\phi_1 = 0.3\) ve \(\theta_1 = -0.8\) için \(Y_t = 0.3Y_{t-1} + \epsilon_t - 0.8\epsilon_{t-1}\) olur.
\(\phi_1 = -0.8\) ve \(\theta_1 = -0.8\) için \(Y_t = -0.8Y_{t-1} + \epsilon_t - 0.8\epsilon_{t-1}\) olur.
\(\phi_1 = 0.8\) ve \(\theta_1 = 0.8\) için \(Y_t = 0.8Y_{t-1} + \epsilon_t + 0.8\epsilon_{t-1}\) olur.
\(\phi_1 = -0.9\) ve \(\theta_1 = 0.8\) için \(Y_t = -0.9Y_{t-1} + \epsilon_t + 0.8\epsilon_{t-1}\) olur.
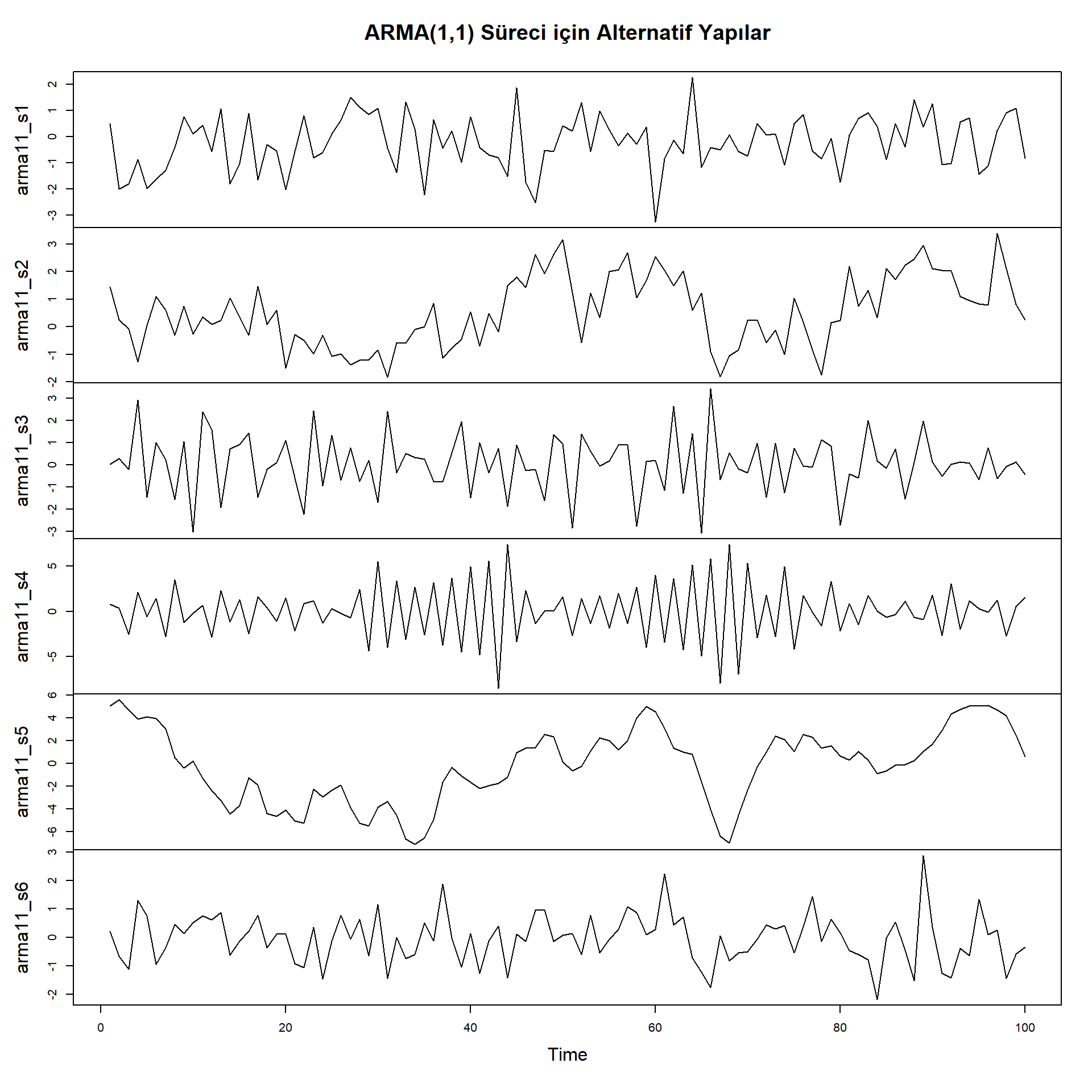
\(\theta_1\) parametresinin değil de \(\phi_1\) parametresinin ki bu otoregresif parametredir, etkili olduğunu görüyoruz. Çünkü, bu parametrenin değeri arttıkça ortalama daha az sayıda kesiliyor.
Homojen Durağan-Dışı Süreçler: ARIMA(p,d,q)
Bu başlığa kadar süreçlerin hep durağan olduğunu varsaydık. Zaman serisi durağan-dışı bir yapıda ise bir ya da birden fazla farkını alarak dönüştürme işlemi gerçekleştiriyoruz. Bu bir entegre süreçtir ve d harfine karşılık gelir. d’nin değeri alınan fark sayıdır.
\(W_t = \Delta^dY_t\) durağan bir seri ise \(Y_t\) serisi d. dereceden homojen durağan-dışıdır.
Süreci iki farklı simülasyon örneği ile görelim.
\(\phi_1=0.5\), \(\theta_1=-0.3\) ve \(\delta = 1\) ise ARIMA(1,1,1)’dir. Yani, ARIMA(p = 1, d = 1, q = 1).

\(\phi_1=0.5\), \(\theta_1=-0.3\) ve \(\delta = 2\) ise ARIMA(1,2,1)’dir. Yani, ARIMA(p = 1, d = 2, q = 1).

ARIMA Model Kurma Süreci: Box-Jenkins Yaklaşımı
Box-Jenkins yaklaşımının temel fikri cimrilik prensibidir. Yani, zaman serisi verilerinin özelliklerini ortaya koyan optimal (minimum sayıda parametre veya serbestlik derecesini göz önünde tutan) bir model kurmayı öngörür.
Yaklaşımı 3 aşamaya ayırabiliriz:
- Tanımlama
1.1. Veri Hazırlama
Varyansı sabitleştirmek için verilere dönüştürme işlemi uygulanır.
Durağan seriyi bulmak için verilerin farkı alınır.
1.2. Model Seçimi
- Potansiyel modelleri teşhis edebilmek için ACF ve PACF hesaplanır.
- Tahmin ve Test Yapma
2.1. Tahmin
Potansiyel modellerdeki parametrelerin tahminleri yapılır.
Uygun kriterler kullanılarak en iyi model seçilir.
2.2. Tanı Kontrol
Kalıntıların ACF/PACF’leri kontrol edilir.
Kalıntıların Portmanteau testleri yapılır.
Kalıntıların temiz-dizi olup olmadığı kontrol edilir.
Modelin yeterliliğine bakılır.
- Uygulama
3.1. Önraporlama
- Önraporlama ve kontrol amacıyla model kullanılır.
Uygulama
2022 için yıl sonu enflasyon öngörüsü yapacağız.
TCMB/EVDS’den aldığım verilere (post8.xlsx) GitHub hesabımdan ulaşabilirsiniz.

Zaman serisi analizlerinin geleneksel yaklaşımında ilk yaptığımız işlem serinin zaman yolu grafiğini çizmektir. Amaç, serinin bir trende sahip olup olmadığını, konjonktürel dalgalanmaların şiddetini, mevsimsel hareketleri incelemek; düzensiz hareketleri gidermektir.
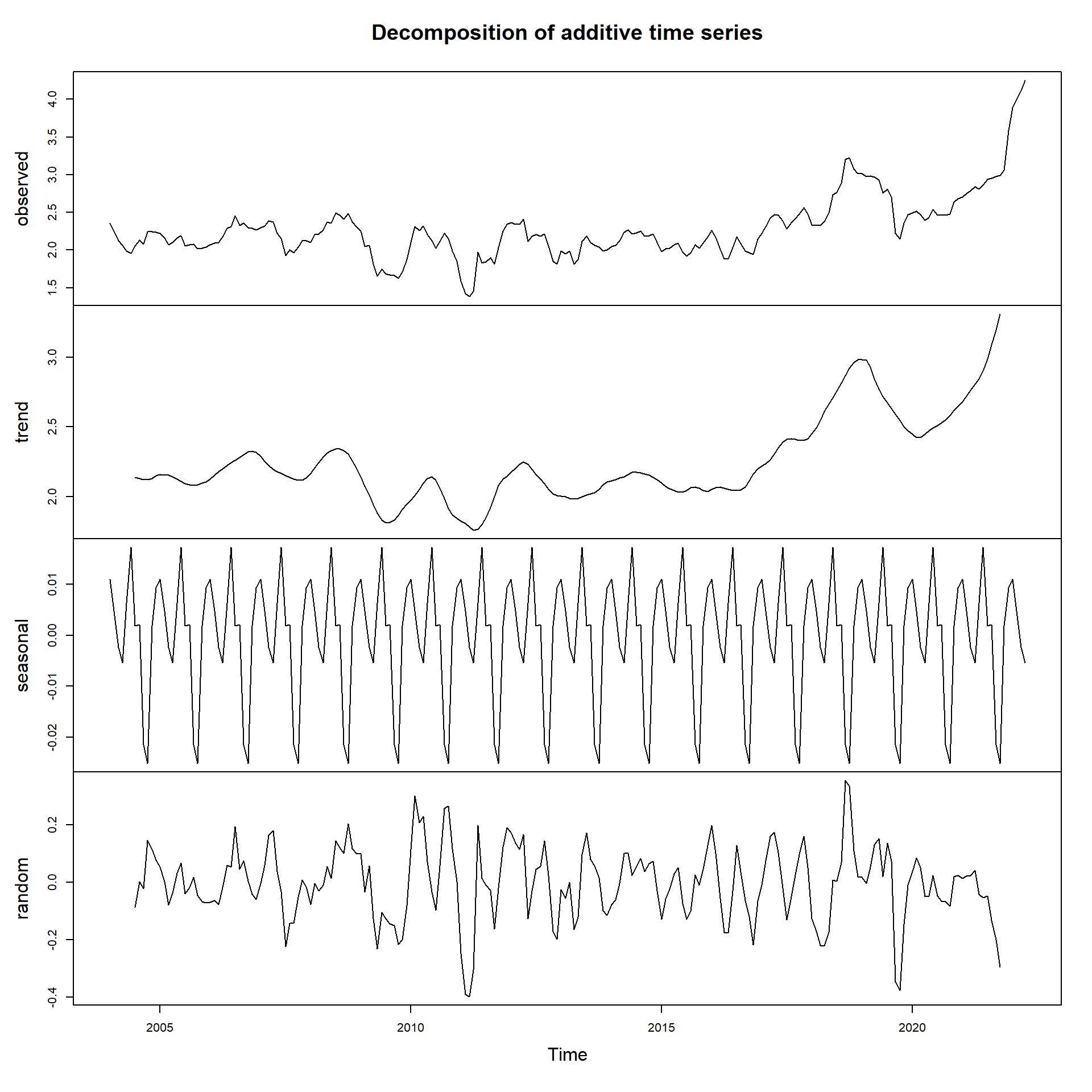
Yazının ilerleyen kısımlarında ayrıştırma işlemi yapmadan R’da bunu dikkate alan fonksiyonu çalıştıracağız.
Biz bu çalışmada model seçimi için Akaike Bilgi Kriteri’ni kullanacağız. Akaike Bilgi Kriteri (AIC) modeldeki terimlerin sayısını dikkate alarak modelin uyumunun iyiliğini ölçen bir kriterdir. AIC = -2LogL + 2m olarak tanımlanır. Burada, L olabilirlik iken; m = p + q’dur. Alternatif tanımlar da mevcuttur.
Alternatif modeller arasında en küçük değerler veren AIC en uygun model ki bu da p ve q, olarak seçilir.
R’da bulunan auto.arima() fonksiyonunu bunun için kullanabiliriz.
Series: enflasyon
ARIMA(2,1,1)(0,0,1)[12] with drift
Coefficients:
ar1 ar2 ma1 sma1 drift
-0.4312 0.1966 0.8280 -0.6551 0.0054
s.e. 0.2036 0.1179 0.1852 0.0606 0.0036
sigma^2 = 0.008768: log likelihood = 206.92
AIC=-401.83 AICc=-401.43 BIC=-381.5
Ljung-Box test
data: Residuals from ARIMA(2,1,1)(0,0,1)[12] with drift
Q* = 10.033, df = 19, p-value = 0.9521
Model df: 5. Total lags used: 24ACF grafiğinde tüm çubukların sınırlar içinde olduğunu görüyoruz. Kalıntılar için beyaz gürültüye uyumlu ya da buna çok yakın diyebiliriz. Kalıntı otokorelasyonlarının baştan sona kabul edilebilirliğinin kontrolü için Ljung-Box testine baktığımızda p değerinin 0.9521 olduğunu görüyoruz. Bu da otokorelasyon olmadığı yönünde bize destek vermektedir. Varsayımlar sağlandı.
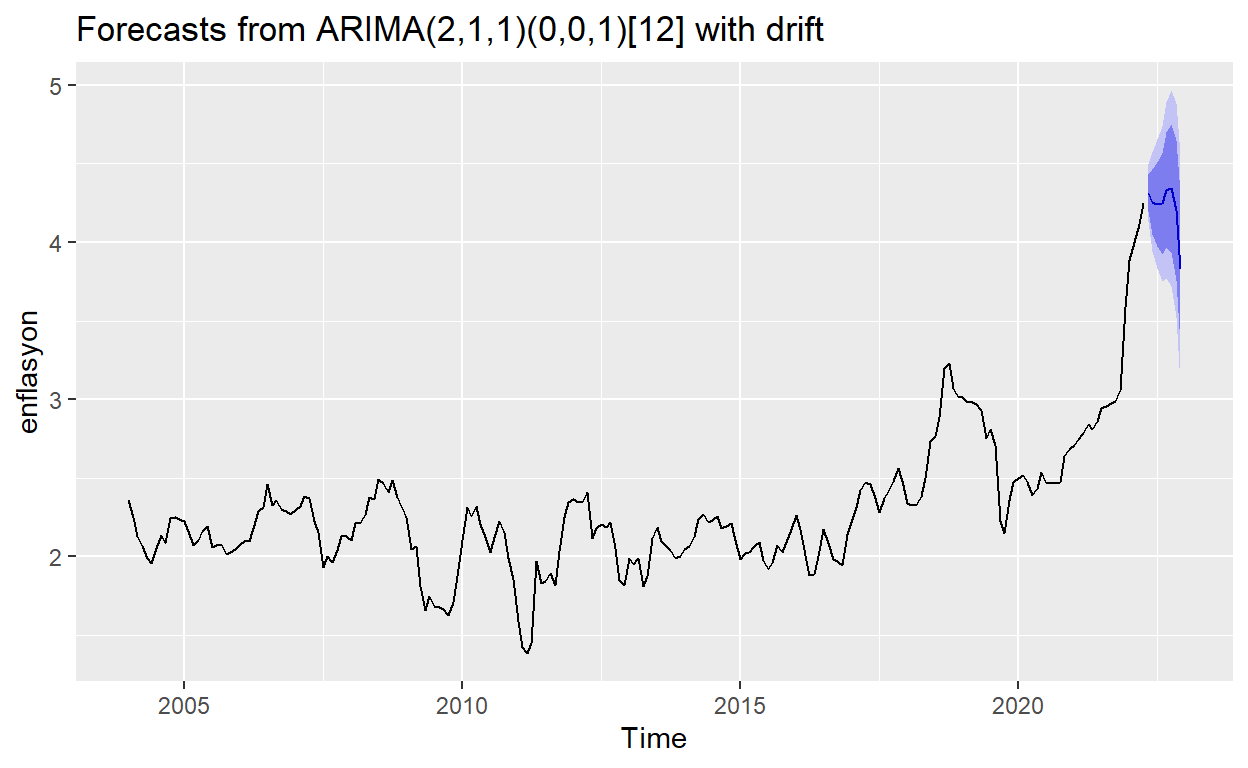
En uygun modelin ARIMA(2,1,1)(0,0,1)[12] olduğunu görüyoruz. ARIMA(p = 2, d = 1, q = 1) kısmını biliyoruz. Peki, (0,0,1)[12] nedir? Serimizde mevsimsellik olduğu için bunu dikkate alan bir model kurduk. Mevsimselliği dikkate aldığımız zaman buna SARIMA diyebiliriz.
\(SARIMA(p,d,q)(P,D,Q)_m\)
p,P: Sırasıyla, mevsimsel olmayan ve olan AR
q,Q: Sırasıyla, mevsimsel olmayan ve olan MA
d,D: Sırasıyla, seri durağan yapılana kadar kaç fark alındı ve seriden mevsimsel etkiyi kaldırmak için kaç fark alındının karşılığıdır.
m: Frekans. Aylık veriler ile çalıştığımız için 12’dir.
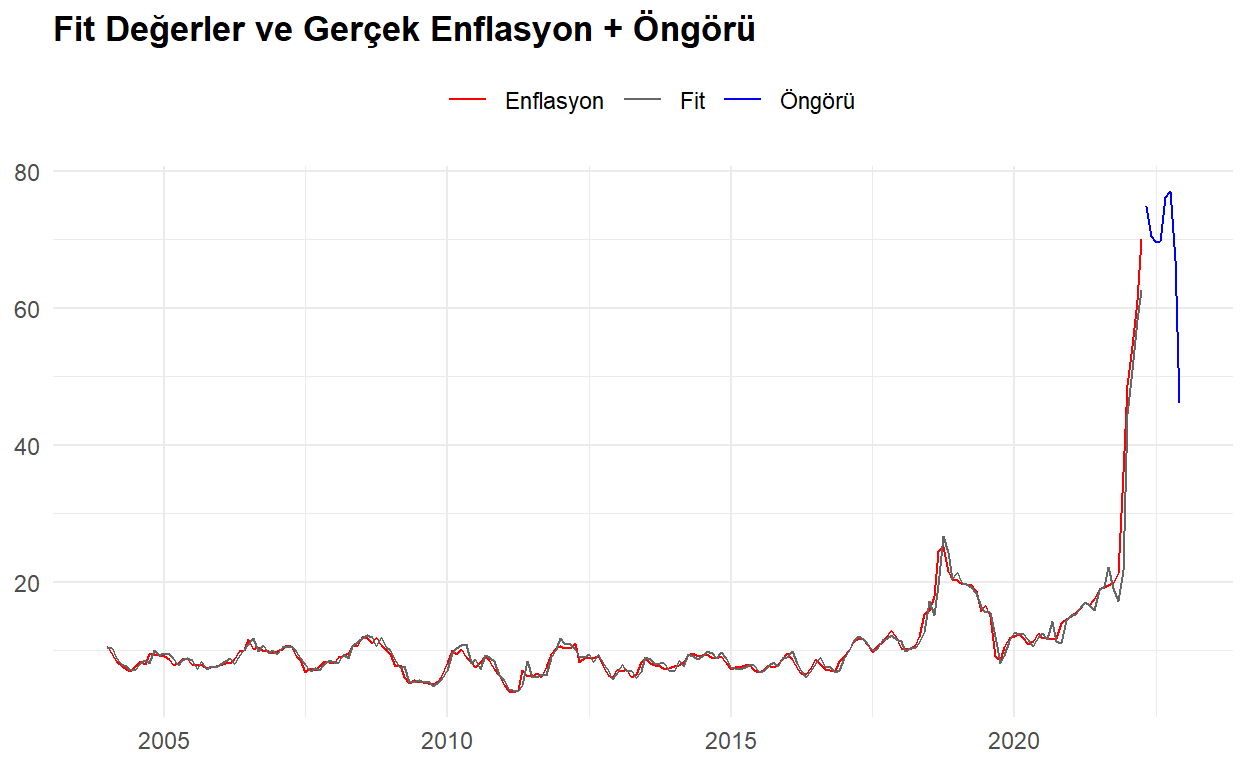
Modele göre enflasyonun Mayıs ayında 74.79% (Alt: 62.25%, Üst: 89.86%); 2022 yılının sonunda ise 46.07% (Alt: 22.14, Üst: 95.85%) olması beklenmektedir. Evet, güven aralığı oldukça geniş ki bu da istenen bir durum olmamalı aslında.
Modele göre enflasyonda beklenen yıl sonu düşüşü beni pek şaşırtmadı. Çünkü, Türkiye’de yarın bile ne olacağını bilemiyoruz (o zaman neden model kuruyoruzun cevabı öngörü heyecanı ve modeli nasıl iyileştirebilirizin sorgulanması). 2021 yılının sonlarına doğru USDTRY’nin yükselişi durdurulamazken bir anda KKM çıktı ve sert bir düşüş gördük. Bakalım enflasyon tarafında ne yaşayacağız.
Son olarak, bu tür çalışmalarda modelin yeni veri geldikçe gözden geçirilmesi ve alternatif yöntemlerle desteklenmesi önemlidir diyebilirim.
| tarih | Öngörü | Alt95 | Üst95 |
|---|---|---|---|
| 2022-05-01 | 74.79428 | 62.25376 | 89.86098 |
| 2022-06-01 | 70.54543 | 51.46939 | 96.69160 |
| 2022-07-01 | 69.65640 | 46.25963 | 104.88657 |
| 2022-08-01 | 69.76207 | 42.64513 | 114.12196 |
| 2022-09-01 | 76.10810 | 43.43605 | 133.35566 |
| 2022-10-01 | 77.00459 | 41.26345 | 143.70364 |
| 2022-11-01 | 66.99449 | 33.93994 | 132.24130 |
| 2022-12-01 | 46.06953 | 22.14357 | 95.84728 |
Çalışmanın R kodlarına aşağıdan ulaşılabilir.
options(scipen = 999)
ar1_s1 <- arima.sim(model = list(ar = 0), n = 100)
ar1_s2 <- arima.sim(model = list(ar = 0.3), n = 100)
ar1_s3 <- arima.sim(model = list(ar = 0.5), n = 100)
ar1_s4 <- arima.sim(model = list(ar = 0.7), n = 100)
ar1_s5 <- arima.sim(model = list(ar = 0.9), n = 100)
plot.ts(cbind(ar1_s1,ar1_s2,ar1_s3,ar1_s4,ar1_s5),
nc = 1,
main = "AR(1) Süreci için Alternatif Yapılar")
ma1_s1 <- arima.sim(model = list(ma = 0), n = 100)
ma1_s2 <- arima.sim(model = list(ma = -0.3), n = 100)
ma1_s3 <- arima.sim(model = list(ma = -0.5), n = 100)
ma1_s4 <- arima.sim(model = list(ma = -0.7), n = 100)
ma1_s5 <- arima.sim(model = list(ma = -0.9), n = 100)
plot.ts(cbind(ma1_s1,ma1_s2,ma1_s3,ma1_s4,ma1_s5),
nc = 1,
main = "MA(1) Süreci için Alternatif Yapılar")
arma11_s1 <- arima.sim(model = list(ar = 0.3, ma = -0.3), n = 100)
arma11_s2 <- arima.sim(model = list(ar = 0.8, ma = -0.3), n = 100)
arma11_s3 <- arima.sim(model = list(ar = 0.3, ma = -0.8), n = 100)
arma11_s4 <- arima.sim(model = list(ar = -0.8, ma = -0.8), n = 100)
arma11_s5 <- arima.sim(model = list(ar = 0.8, ma = 0.8), n = 100)
arma11_s6 <- arima.sim(model = list(ar = -0.9, ma = 0.8), n = 100)
plot.ts(cbind(arma11_s1,arma11_s2,arma11_s3,arma11_s4,arma11_s5,arma11_s6),
nc = 1,
main = "ARMA(1,1) Süreci için Alternatif Yapılar")
arima111_s1 <- arima.sim(model = list(order = c(1,1,1), ar = 0.5, ma = -0.3), n = 100)
plot.ts(arima111_s1, main = "ARIMA(1,1,1)")
arima121_s1 <- arima.sim(model = list(order = c(1,2,1), ar = 0.5, ma = -0.3), n = 100)
plot.ts(arima121_s1, main = "ARIMA(1,2,1)")
library(tidyverse)
library(forecast)
df <- readxl::read_excel("data.xlsx") %>%
mutate(tarih = as.Date(paste0(tarih,"-",1)),
lenf = log(enf))
enflasyon <- ts(data = df$lenf,
start = c(2004,1),
end = c(2022,4),
frequency = 12)
ggplot(df, aes(x = tarih, y = lenf)) +
geom_line() +
theme_minimal() +
theme(axis.title = element_blank(),
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(face = "italic"),
plot.caption = element_text(face = "italic")) +
labs(
title = "Enflasyon*, 2004/Ocak-2022/Nisan",
subtitle = "*Bir önceki yılın aynı ayına göre değişim",
caption = "Serinin logaritması alınmıştır."
)
plot(decompose(enflasyon))
model <- auto.arima(y = enflasyon, ic = "aic") # trace = TRUE olursa tüm modeller izlenebilir
model
checkresiduals(model)
ongoru <- forecast(model, h = 8) # Mayıs-Aralık = 8 ay
model_output <- data.frame(
tarih = df$tarih,
Fit = model$fitted,
Enflasyon = model$x
) %>%
bind_rows(
data.frame(
tarih = seq(as.Date("2022-05-01"),as.Date("2022-12-01"),by = "months"),
Fit = rep(NA,8),
Enflasyon = rep(NA,8)
)
) %>%
mutate(`Öngörü` = c(rep(NA,220),ongoru$mean),
`Alt95` = c(rep(NA,220),ongoru$lower[,2]),
`Üst95` = c(rep(NA,220),ongoru$upper[,2])) %>%
pivot_longer(!tarih, names_to = "var", values_to = "val")
ggplot(model_output %>% filter(!(var %in% c("Alt95","Üst95"))),
aes(x = tarih, y = exp(val), color = var)) +
geom_line() +
theme_minimal() +
theme(axis.title = element_blank(),
legend.title = element_blank(),
legend.position = "top",
plot.title = element_text(face = "bold")) +
scale_color_manual(values = c("red","gray40","blue","gray","gray")) +
labs(title = "Fit Değerler ve Gerçek Enflasyon + Öngörü")
autoplot(forecast(model, h = 8))
Yararlandığım Kaynaklar:
Ekonometrik Zaman Serileri Analizi; M.Sevüktekin, M.Çınar
ZAMAN SERİLERİ ANALİZİNDE ARIMA MODELLERİ VE BİR UYGULAMA; Ö.Duru