Markov süreci, bir stokastik sürecin şu anki değerleri bilindiğinde, sürecin gelecekteki değerlerinin geçmişteki değerlerinden koşullu olarak bağımsız olduğu süreçtir. Markov zinciri ise Markov sürecinin kesikli durum uzayına sahip olduğu özel bir durumdur. Stokastik sistemlerin kısa veya uzun dönemdeki davranışlarının modellenmesinde Markov zincirlerinden yararlanılmaktadır.
Aylık frekansta olan ve Haziran 2018 (başkanlık sistemi) ile Nisan 2022 (son veri) arasını kapsayan verileri TCMB/EVDS’den aldım. Faizi temsilen Ağırlık Ortalama Fonlama Maliyeti’ni; enflasyonu temsilen de TÜFE’den elde edilen yıllık değişimleri kullandım. Verilere (post3.xlsx) GitHub hesabımdan ulaşabilirsiniz.
library(kableExtra) # zorunlu değil
library(expm) # %^% operatörü
library(markovchain) # uzun dönem denge hesaplaması
library(tidyverse)
library(ggalluvial)
df <- readxl::read_excel("data.xlsx")
df <- df %>%
mutate(tarih = as.Date(paste0(tarih,"-",1))) %>%
filter(tarih >= as.Date("2018-06-01")) %>%
na.omit() # Mayıs 2022 verisi çıkarıldı.

Elimizdeki durumların (State; S1, S2, …) neler olabileceğine bakalım:
S1: Faiz Yükseldi - Enflasyon Yükseldi
S2: Faiz Yükseldi - Enflasyon Düştü
S3: Faiz Düştü - Enflasyon Yükseldi
S4: Faiz Düştü - Enflasyon Düştü
S5: Faiz Değişmedi - Enflasyon Yükseldi
S6: Faiz Değişmedi - Enflasyon Düştü
df2 <- df %>%
mutate(
durum = case_when(
lead(faiz) > faiz & lead(enflasyon) > enflasyon ~ "S1",
lead(faiz) > faiz & lead(enflasyon) < enflasyon ~ "S2",
lead(faiz) < faiz & lead(enflasyon) > enflasyon ~ "S3",
lead(faiz) < faiz & lead(enflasyon) < enflasyon ~ "S4",
lead(faiz) == faiz & lead(enflasyon) > enflasyon ~ "S5",
lead(faiz) == faiz & lead(enflasyon) < enflasyon ~ "S6",
) # lead() ---> bir sonraki durum; t + 1 ile t karşılaştırılıyor
) %>%
na.omit() %>% # NA içeren değerler çıkarıldı
select(durum) # yeterli olacak sütun
Kesikli parametreli Markov zincirlerinde sistem belirli bir olasılık dağılımına bağlı olarak bulunduğu durumdan başka bir duruma geçebilir veya aynı durumda kalabilir. Bu nedenle, incelenen sistemin içinde bulunabileceği farklı durumların ve bu durumların birinden diğerine geçiş olasılıklarını bilmemiz gerekir. Sistemin bu durum değişiklikleri geçiş olarak isimlendirilir ve durum uzayındaki herhangi i ve j durumları için, \(p_{ij}(m,n) = P(X_{m+n} = j/X_m = i)\) biçimindeki koşullu olasılığa geçiş olasılığı adı verilir. Ayrıca, homojen bir Markov zincirinde geçiş olasılığı yalnızca adım sayısının bir fonksiyonudur ve m zamanına bağlı değildir.
Yukarıdaki durumları baz alarak Markov geçiş matrisini oluşturalım.
Tabloda olmayan bazı durumlar var. Bunları tüm durumları baz alarak ekleyebiliriz.
Matrisi oluşturabiliriz. Her bir hücreyi o satırın toplamına bölerek olasılıkları hesaplayacağız.
m <- tumDurumlar %>%
pivot_wider(names_from = "durum2", values_from = "n") %>% # sütun
column_to_rownames(var = "durum") %>% # satır
mutate_all(.funs = function(x) round(x / rowSums(.), digits = 2)) %>%
mutate_if(is.numeric, funs(ifelse(is.nan(.), 0, .))) %>%
as.matrix()
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| S1 | 0.38 | 0.12 | 0.25 | 0.12 | 0.12 | 0.00 |
| S2 | 0.50 | 0.00 | 0.25 | 0.25 | 0.00 | 0.00 |
| S3 | 0.07 | 0.07 | 0.47 | 0.13 | 0.13 | 0.13 |
| S4 | 0.00 | 0.14 | 0.43 | 0.43 | 0.00 | 0.00 |
| S5 | 0.12 | 0.00 | 0.12 | 0.00 | 0.62 | 0.12 |
| S6 | 0.33 | 0.33 | 0.00 | 0.00 | 0.33 | 0.00 |
Yukarıdaki matris bir-adım geçiş olasılığı matrisidir. Homojen bir Markov zincirinde m. adımda i durumunda bulunan sürecin bir adım sonra j durumunda bulunması olasılığı \(p_{ij} = p_{ij}(1) = p_{ij}^{(1)} = P(X_{m+1} = j/X_m = i)\)’dir. Yukarıdaki bir-adım geçiş matrisinde satırlar sistemin şu an bulunabileceği durumları; sütunlar ise bir adım sonra bulunabileceği durumları göstermektedir.
Başlangıç durumu S5’tir. Yani, faiz değişmedi - enflasyon yükseldi. Gelecek Mayıs ayına ait olasılıklara bakalım.
baslangicDurum %*% m
| S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|
| 0.12 | 0 | 0.12 | 0 | 0.62 | 0.12 |
Faizin değişmediği ve enflasyonun yükseldiği bir dönemden yine faizin değişmediği ve enflasyonun yükseldiği bir döneme geçiş olasılığı 62%’dir.
Peki, Haziran ayı için (iki-adım geçiş) olasılıklar ne olacaktır?
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| S1 | 0.24 | 0.08 | 0.31 | 0.16 | 0.15 | 0.05 |
| S2 | 0.21 | 0.11 | 0.35 | 0.20 | 0.09 | 0.03 |
| S3 | 0.15 | 0.10 | 0.33 | 0.14 | 0.19 | 0.08 |
| S4 | 0.10 | 0.09 | 0.42 | 0.28 | 0.06 | 0.06 |
| S5 | 0.17 | 0.06 | 0.16 | 0.03 | 0.45 | 0.09 |
| S6 | 0.33 | 0.04 | 0.20 | 0.12 | 0.24 | 0.04 |
Markov zincirinde ilk olasılık dağılımı ve zincirin bir-adım geçiş matrisini belirlediğimizde zincirin tüm adımlarındaki olasılıkları kolayca elde edebiliriz. n-adım olasılıklı vektörü \(\pi_{n} = \pi_{n-1}P\) olsun. Buradan aşağıdaki eşitlikleri türetebiliriz.
\(\pi_n = (\pi_{n-2}P)P = \pi_{n-2}P^2\)
.
.
.
\(\pi_n = \pi_0P^n\)
P geçiş matrisinin n. kuvvetini aldığımızda elde edeceğimiz n-adım geçiş matrisi \(P^n\)’de n değeri büyüdükçe \(P_{ij}^{(n)}\) olasılık değerleri sabit bir değere ya da limite yaklaşıyorsa, n-adım geçiş olasılıkları denge durumuna ulaşır. Denge durumuna ulaştığımızda geçiş matrisinin satırlarında değişim olmadığını göreceğiz. Yani, her satırı aynı olan bir geçiş matrisi elde edeceğiz.
\(\pi_n = [\pi_0 \pi_1 ... \pi_n]\)
m <- tumDurumlar %>%
pivot_wider(names_from = "durum2", values_from = "n") %>% # sütun
column_to_rownames(var = "durum") %>% # satır
mutate_all(.funs = function(x) x / rowSums(.)) %>%
# satır toplamı 1 olması için round() kaldırıldı
mutate_if(is.numeric, funs(ifelse(is.nan(.), 0, .))) %>%
as.matrix()
n_adim <- new(
"markovchain",
transitionMatrix = matrix(as.numeric(m), nrow = 6, ncol = 6)
)
steadyStates(n_adim) %>% round(. ,digits = 2)
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 0.18 | 0.09 | 0.29 | 0.15 | 0.23 | 0.07 |
Uzun dönemde;
Faizin yükseldiği ve enflasyonun yükseldiği dönem olasılığı 18%,
Faizin yükseldiği ve enflasyonun düştüğü dönem olasılığı 9%,
Faizin düştüğü ve enflasyonun yükseldiği dönem olasılığı 29%,
Faizin düştüğü ve enflasyonun düştüğü dönem olasılığı 15%,
Faizin değişmediği ve enflasyonun yükseldiği dönem olasılığı 23%,
Faizin değişmediği ve enflasyonun düştüğü dönem olasılığı 7%’dir.
Değerlerin toplamı yuvarlamadan dolayı 100% değildir.
Yukarıdaki olasılıkları baz aldığımızda uzun vadede enflasyonun yükselmesi olasılığı 70% iken; düşmesi olasılığı 30%’dur.
Görsellere ait kodlara aşağıdan ulaşılabilir.
df %>%
rename("AOFM"=2, "Enflasyon"=3) %>%
pivot_longer(!tarih, names_to = "variables", values_to = "values") %>%
ggplot(aes(x = tarih, y = log(values), group = variables, color = variables)) +
geom_line() +
theme_minimal() +
theme(axis.title = element_blank(),
legend.title = element_blank(),
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(face = "italic", size = 7),
plot.caption = element_text(face = "italic", size = 5)) +
scale_color_manual(values = c("blue","red")) +
labs(title = "Ağırlıklı Ortalama Fonlama Faizi ve Enflasyon (YoY)",
subtitle = "Ocak 2011 - Nisan 2022",
caption = "Değerler logaritmiktir.\nVeriler TCMB/EVDS'den alınmıştır.")
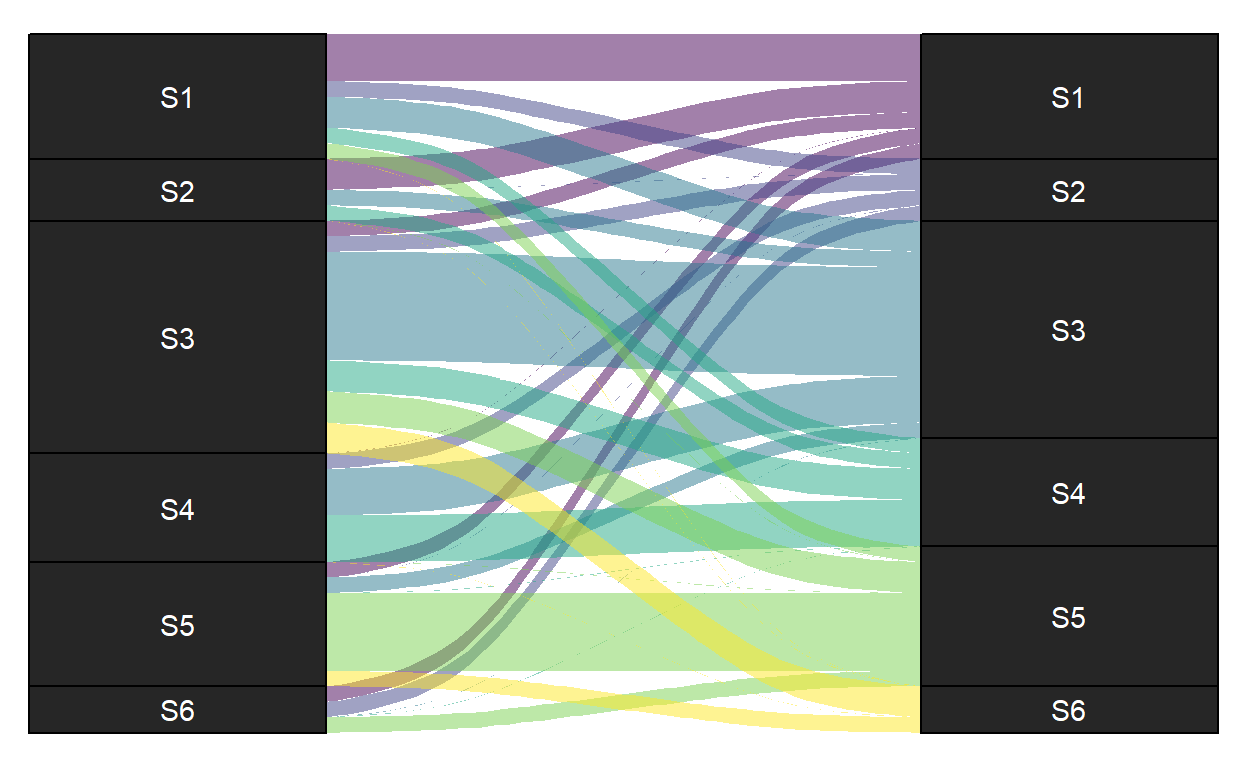
ggplot(data = tumDurumlar, aes(axis1 = durum, axis2 = durum2, y = n)) +
geom_alluvium(aes(fill = durum2)) +
geom_stratum(fill = "gray15") +
geom_text(stat = "stratum", aes(label = after_stat(stratum)), color = "white") +
scale_x_discrete(limits = c("durum", "durum2"), expand = c(0.15, 0.05)) +
theme_void() +
theme(legend.position = "none") +
scale_fill_viridis_d()
Yararlandığım Kaynaklar:
Stokastik Süreçler ve R Uygulamaları; G.Ö.Kadılar