Futbol Maçları İçin Daha İyi Tahminler: Dixon-Coles Modeli Nasıl Çalışır?

Dixon-Coles Modeli

Mark J. Dixon ve Stuart G. Coles (1997) tarafından geliştirilen model, geleneksel Poisson regresyonuna bir düzeltme faktörü ekleyerek düşük skorlu maçlardaki bağımlılıkları daha iyi modellemeyi amaçlamaktadır. Bu model, özellikle nadir skorların tahmin doğruluğunu artırarak, bu alanda önemli bir yere sahip olmuştur.

Dixon ve Coles’un Modelling Association Football Scores and Inefficiencies in the Football Betting Market başlıklı çalışması, bu metodolojinin temel taşlarını oluşturur. Model, takımların hücum ve savunma gücünü tahmin etmeye dayanarak, belirli bir maç için olası skor dağılımlarını hesaplamayı hedefler.

Bu yazıda, Dixon-Coles modelinin teorik temellerini ayrıntılı bir şekilde inceleyeceğiz. Modelin matematiksel yapısını açıklayarak, parametre tahmin süreçlerine değinecek ve modelin Python ile nasıl uygulanacağını adım adım göreceğiz. Uygulama sürecinde, veri setinin nasıl hazırlanacağı, modelin nasıl optimize edileceği ve sonuçların nasıl yorumlanması gerektiği gibi konulara odaklanacağız.

Dixon-Coles Modelinin Teorik Temelleri

Dixon-Coles modeli, futbol maçı sonuçlarının tahmininde Poisson dağılımına dayanan istatistiksel bir yaklaşımdır. Model, her takımın hücum ve savunma yetkinliklerini matematiksel parametreler aracılığıyla temsil eder ve bu parametreleri kullanarak belirli bir maçtaki potansiyel skor dağılımlarını hesaplar. Geleneksel Poisson modelinin aksine, Dixon-Coles modeli düşük skorlu maçlardaki bağımlılıkları daha iyi yakalamak için ek bir düzeltme faktörü içerir. Böylece, modelin tahmin doğruluğu artırılarak daha gerçekçi sonuçlar elde edilmesi sağlanır.

Poisson Dağılımı ve Futbol Maçları

Poisson dağılımı, belirli bir zaman aralığında meydana gelen olayların sayısını modellemek için kullanılır ve futbol maçlarında bir takımın attığı gol sayısı için sıkça tercih edilir. Ancak, geleneksel Poisson modeli, takımların gol atma eğilimlerini birbirinden bağımsız olarak ele alır. Dixon ve Coles, düşük skorlu maçlarda bu bağımsızlık varsayımının geçerli olmadığını göstererek modelde bir düzeltme faktörü (\(\tau\)) önermiştir.

Bir takımın gol atma olasılığı şu şekilde ifade edilir:

\(P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}\)

Burada:

• \(λ\): Takımın ortalama gol sayısı
• \(k\): Takımın attığı gol sayısı

Dixon-Coles Modelinin Parametreleri

Dixon-Coles modeli, her takımın hücum gücünü (\(\alpha\)) ve savunma gücünü (\(\beta\)) tahmin etmek için geliştirilmiş bir Poisson tabanlı regresyon modelidir. Ek olarak, ev sahibi avantajı (\(\gamma\)) da modele dahil edilir. Modelin özgün katkısı ise takımların gol atma eğilimleri arasındaki bağımlılığı düzeltmek için eklenen \(\tau\) düzeltme faktörüdür. Bu düzeltme faktörü, özellikle düşük skorlu maçları (örn. 0-0, 1-0, 0-1, 1-1) daha iyi modellemeyi amaçlar.

Modelin Matematiksel Formülasyonu

Dixon-Coles modeli, ev sahibi takımın gol sayısı \(X\) ve deplasman takımının gol sayısı \(Y\) için Poisson dağılımını temel alır. Ancak, geleneksel Poisson modelinden farklı olarak \(\tau\) düzeltme faktörü kullanılır:

\(P(X=x, Y=y) = \tau_{\lambda,\mu}(x,y)\frac{e^{-\lambda}\lambda^x}{x!}\frac{e^{-\mu}\mu^y}{y!}\)

Burada:

• \(\lambda\): Ev sahibi takımın gol beklentisi
• \(\mu\): Deplasman takımının gol beklentisi
• \(\tau_{\lambda,\mu}(x,y)\): Düşük skorlu maçlarda bağımlılığı hesaba katan düzeltme faktörü

Dixon-Coles, \(\tau\) faktörünün özellikle 0-0, 1-0, 0-1 ve 1-1 skorlarında büyük bir etki yarattığını ve klasik Poisson modeline kıyasla daha iyi sonuçlar verdiğini göstermiştir.

Ev sahibi takımın ortalama gol sayısı \(\lambda\) ve deplasman takımının ortalama gol sayısı \(\mu\), takımların hücum ve savunma güçleri ile ev sahibi avantajı kullanılarak hesaplanır:

\(\lambda = \alpha_i \beta_j \gamma\)

\(\mu = \alpha_j \beta_i\)

Burada:

• \(\alpha_i\): Ev sahibi takımın hücum gücü
• \(\beta_j\): Deplasman takımının savunma gücü
• \(\gamma\): Ev sahibi avantajı

Düzeltme Faktörü \(\tau_{\lambda,\mu}(x,y)\)

Dixon-Coles modeli, özellikle düşük skorlu maçlarda (0-0, 1-0 gibi) bağımlılığı modellemek için bir düzeltme faktörü kullanır. Bu faktör, maçlar arasındaki bağımlılığı ifade eder ve şu şekilde tanımlanır:

\[ \tau_{\lambda, \mu}(x, y) = \begin{cases} 1 - \lambda \mu \rho & \text{if } x = y = 0, \\ 1 + \lambda \rho & \text{if } x = 0, y = 1, \\ 1 + \mu \rho & \text{if } x = 1, y = 0, \\ 1 - \rho & \text{if } x = y = 1, \\ 1 & \text{diğer durumlarda}. \end{cases} \]

Burada \(\rho\), bağımlılık parametresidir.

Uygulama

2024/25 Sezonu 24. Hafta Tahminleri

Dixon-Coles modelini Python kullanarak nasıl uygulayabileceğimizi adım adım inceleyelim.

Gerekli Kütüphanelerin Yüklenmesi

Öncelikle, ihtiyacımız olan kütüphaneleri yükleyelim. Bu kütüphaneler, matematiksel hesaplamalar, veri işleme ve optimizasyon işlemleri için kullanılacaktır.

import numpy as np
import pandas as pd
from scipy.optimize import minimize, Bounds
from scipy.stats import poisson

Veri Setinin Hazırlanması

Modeli uygulamak için veri setinin temelde, ev sahibi ve deplasman takımlarını ve skorlarını içermesi gerekiyor. Hedef veri setine buradan ulaşabilirsiniz.

df = pd.read_json("./data/tff_super_lig_2425_1-23_maclar.json", lines=True)

Bu kod, JSON formatındaki veri setini bir pandas DataFrame’ine yükler.

rho_correction Fonksiyonu

\[ \tau_{\lambda, \mu}(x, y) = \begin{cases} 1 - \lambda \mu \rho & \text{if } x = y = 0, \\ 1 + \lambda \rho & \text{if } x = 0, y = 1, \\ 1 + \mu \rho & \text{if } x = 1, y = 0, \\ 1 - \rho & \text{if } x = y = 1, \\ 1 & \text{diğer durumlarda}. \end{cases} \]

def rho_correction(x, y, lambda_x, mu_y, rho):
    if x == 0 and y == 0:
        return max(1 - lambda_x * mu_y * rho, 1e-10)
    elif x == 0 and y == 1:
        return 1 + lambda_x * rho
    elif x == 1 and y == 0:
        return 1 + mu_y * rho
    elif x == 1 and y == 1:
        return max(1 - rho, 1e-10)
    else:
        return 1.0

Bu fonksiyon, Dixon-Coles modelinde kullanılan \(\tau_{\lambda,\mu}(x,y)\) düzeltme faktörünü hesaplıyor.

• Poisson dağılımı bağımsızlık varsayımı yapar ancak Dixon-Coles modelinde düşük skorlu maçlarda bağımlılık olduğu kabul edilir.
• \(\rho\) parametresi bu bağımlılığı hesaba katmak için kullanılır
• max(1e-10) gibi bir değer hesaplama sırasında sıfıra bölünme hatalarını önlemek için eklendi.

dc_log_like Fonksiyonu

\(logP(X=x, Y=y) = log(\tau_{\lambda,\mu}(x,y))log(\frac{e^{-\lambda}\lambda^x}{x!})log(\frac{e^{-\mu}\mu^y}{y!})\)

def dc_log_like(x, y, alpha_x, beta_x, alpha_y, beta_y, rho, gamma):
    lambda_x = np.exp(alpha_x + beta_y + gamma)
    mu_y = np.exp(alpha_y + beta_x)
    log_lambda_x = np.log(max(poisson.pmf(x, lambda_x), 1e-10))
    log_mu_y = np.log(max(poisson.pmf(y, mu_y), 1e-10))
    return (
        np.log(max(rho_correction(x, y, lambda_x, mu_y, rho), 1e-10)) + log_lambda_x + log_mu_y
    )

Bu fonksiyon, log-likelihood (olabilirlik) fonksiyonunu hesaplar.

• \(\lambda_x\) ve \(\mu_y\), takımların gol beklentilerini ifade eder.
• Poisson olasılıkları hesaplanır ve logaritmaya alınarak çok küçük değerlerin hata üretmesi önlenir ve hesaplamalar sayısal olarak daha stabil hale getirilir.
• Düzeltme faktörü \(\tau\) hesaba katılır, böylece Dixon-Coles modeli klasik Poisson modeline göre daha iyi bir tahmin yapabilir.

solve_parameters Fonksiyonu

def solve_parameters(dataset, init_vals=None, options={"disp": True, "maxiter": 100}, **kwargs):
    teams = np.sort(
        list(
            set(dataset["home_team"].unique()) | set(dataset["away_team"].unique())
        )
    )
    n_teams = len(teams)

    if init_vals is None:
        avg_attack = dataset.groupby("home_team")["home_score"].mean().reindex(teams).fillna(1.0).values
        avg_defence = -dataset.groupby("away_team")["away_score"].mean().reindex(teams).fillna(1.0).values
        init_vals = np.concatenate([
            avg_attack,
            avg_defence,
            np.array([0, 1.0])
        ])

    def estimate_parameters(params):
        attack_coeffs = dict(zip(teams, params[:n_teams]))
        defence_coeffs = dict(zip(teams, params[n_teams:2 * n_teams]))
        rho, gamma = params[-2:]

        log_likelihoods = [
            dc_log_like(
                row.home_score,
                row.away_score,
                attack_coeffs[row.home_team],
                defence_coeffs[row.home_team],
                attack_coeffs[row.away_team],
                defence_coeffs[row.away_team],
                rho, gamma
            )
            for row in dataset.itertuples()
        ]
        return -np.sum(log_likelihoods)

    constraints = [{"type": "eq", "fun": lambda x, n=n_teams: sum(x[:n]) - n}]

    bounds = Bounds(
        [-np.inf] * n_teams + [-np.inf] * n_teams + [-1, 0],
        [np.inf] * n_teams + [np.inf] * n_teams + [1, np.inf]
    )

    opt_output = minimize(estimate_parameters, init_vals, options=options, constraints=constraints, bounds=bounds, **kwargs)

    return dict(
        zip(
            ["attack_" + team for team in teams] +
            ["defence_" + team for team in teams] +
            ["rho", "home_adv"],
            opt_output.x
        )
    )

Bu fonksiyon, Dixon-Coles modelinin parametrelerini tahmin etmek için optimizasyon işlemi yapar.

Önce, her takım için saldırı (\(\alpha\)) ve savunma (\(\beta\)) katsayıları, ev sahibi avantajı (\(\gamma\)) ve bağımlılık parametresi (\(\rho\)) optimize edilir.

Optimizasyon süreci, şu log-likelihood fonksiyonunu maksimize etmek için çalışır:

\(\sum_{i=1}^{N}=logP(X_i=x_i, Y_i=y_i)\)

• Takımların ortalama hücum ve savunma güçleri başlangıç değerleri olarak alınır.
• \(\rho\) ve \(\gamma\) gibi genel katsayılar da optimize edilir.

dixon_coles_simulate_match Fonksiyonu

def dixon_coles_simulate_match(params_dict, home_team, away_team, max_goals=10):
    def calc_means(param_dict, home_team, away_team):
        return [
            np.exp(param_dict["attack_" + home_team] + param_dict["defence_" + away_team] + param_dict["home_adv"]),
            np.exp(param_dict["defence_" + home_team] + param_dict["attack_" + away_team])
        ]

    team_avgs = calc_means(params_dict, home_team, away_team)
    team_pred = [[poisson.pmf(i, team_avg) for i in range(max_goals + 1)] for team_avg in team_avgs]

    output_matrix = np.outer(np.array(team_pred[0]), np.array(team_pred[1]))

    correction_matrix = np.array([
        [rho_correction(h, a, team_avgs[0], team_avgs[1], params_dict["rho"]) for a in range(2)]
        for h in range(2)
    ])
    output_matrix[:2, :2] *= correction_matrix

    return output_matrix

Bu fonksiyon, belirli bir maçın skor olasılıklarını hesaplar.

Adımlar:

1. Poisson dağılımı kullanılarak her takımın belirli sayıda gol atma olasılıkları hesaplanır.

2. Bu olasılıklar bir matris (çarpım tablosu) şeklinde düzenlenir.

3. Dixon-Coles düzeltme faktörü (\(\tau\)) eklenerek, düşük skorlu sonuçlar daha iyi modellenir.

Matematiksel olarak:

\(P(X=x, Y=y) = \tau_{\lambda,\mu}(x,y)P(X=x)P(Y=y)\)

Burada \(P(X = x)\) ve \(P(Y = y)\), klasik Poisson olasılıklarıdır.

• \(\tau\) düzeltmesi sadece (0-0, 1-0, 0-1, 1-1) skorlarına uygulanıyor. Dixon-Coles’un orijinal çalışmasında bu düzeltme yalnızca bu skorlar için önerildiği için bu kısıtlama doğrudur.

Yukarıdaki fonksiyonları aşağıdaki gibi özetleyebiliriz.

Fonksiyon	Dixon-Coles Modelindeki Karşılığı
rho_correction	\(\tau_{\lambda, \mu}(x, y)\) düzeltme faktörünü hesaplar.
dc_log_like	Log-likelihood fonksiyonunu hesaplar.
solve_parameters	\(\alpha\), \(\beta\), \(\rho\), \(\gamma\) parametrelerini optimize eder.
dixon_coles_simulate_match	Bir maçın skor olasılıklarını hesaplar ve Dixon-Coles düzeltmesini uygular.

Kodun Çalıştırılması

params_dict = solve_parameters(df)

Parametrelerin Yorumlanması

Yukarıdaki değerleri grafik üzerinde görelim.

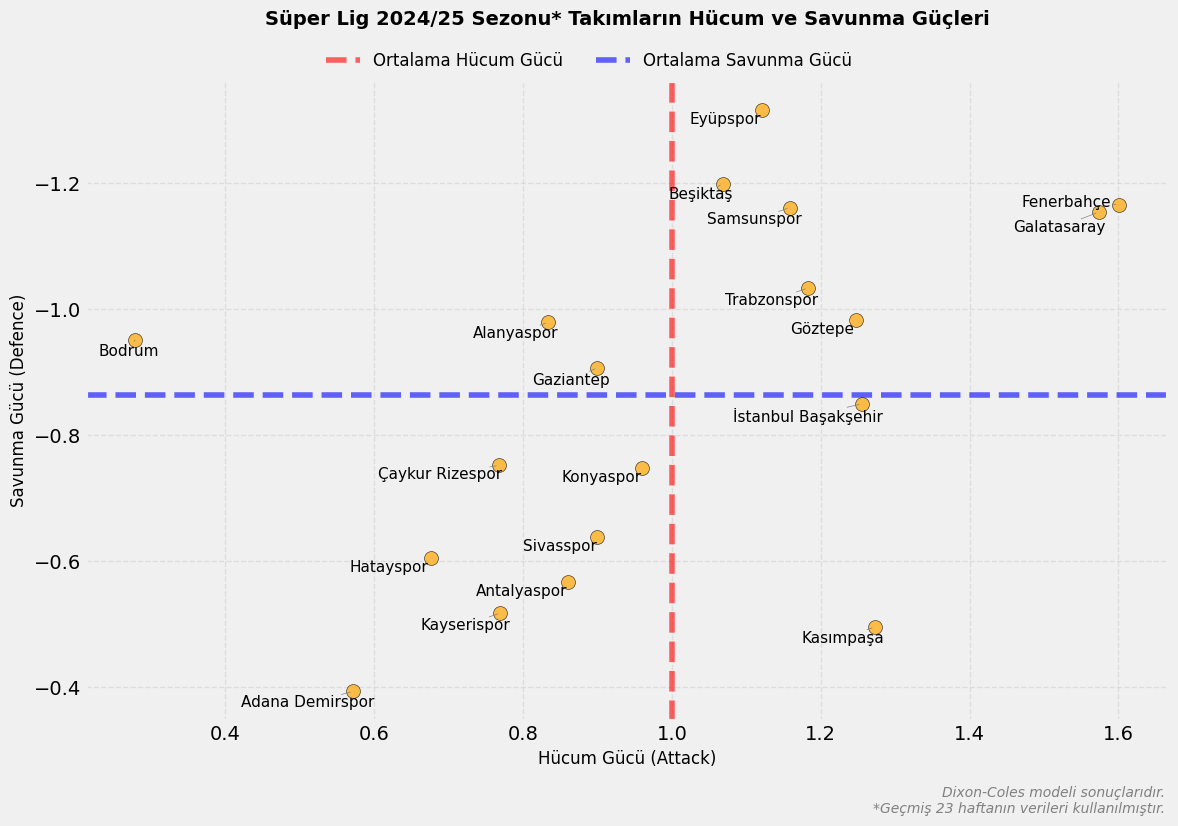
Takımların Hücum Güçleri (attack_*)

Her takımın hücum gücü (attack), gol atma potansiyelini gösterir.

• Pozitif değerler: Lig ortalamasının üzerinde hücum gücüne sahip takımlar.
• Negatif değerler: Lig ortalamasının altında hücum gücüne sahip takımlar.

Takımların Savunma Güçleri (defence_*)

Her takımın savunma gücü (defence), rakipleri ne kadar durdurabildiğini gösterir.

• Negatif değerler: Daha iyi savunma yapan (az gol yiyen) takımlar.
• Pozitif değerler: Daha kötü savunma yapan (çok gol yiyen) takımlar.

Ev Sahibi Avantajı (home_adv)

• Ev sahibi avantajı (home_adv) = 0.2852
• Bu değer, ev sahibi takımın gol beklentisini artıran bir faktördür.
• Yani, ev sahibi olan bir takımın hücum gücü yaklaşık %28 daha yüksek olarak tahmin edilmektedir.

Bağımlılık Parametresi (\(\rho\))

• \(\rho\) değeri = -0.2242
• Negatif \(\rho\) değeri, düşük skorlu maçların beklenenden daha sık olduğunu gösterir.
• Örneğin, 0-0 ve 1-1 skorları, klasik Poisson modeline göre daha olası.

Sonuçların Görselleştirilmesi

home_team = "Adana Demirspor"
away_team = "Antalyaspor"
match_matrix = dixon_coles_simulate_match(params_dict, home_team, away_team)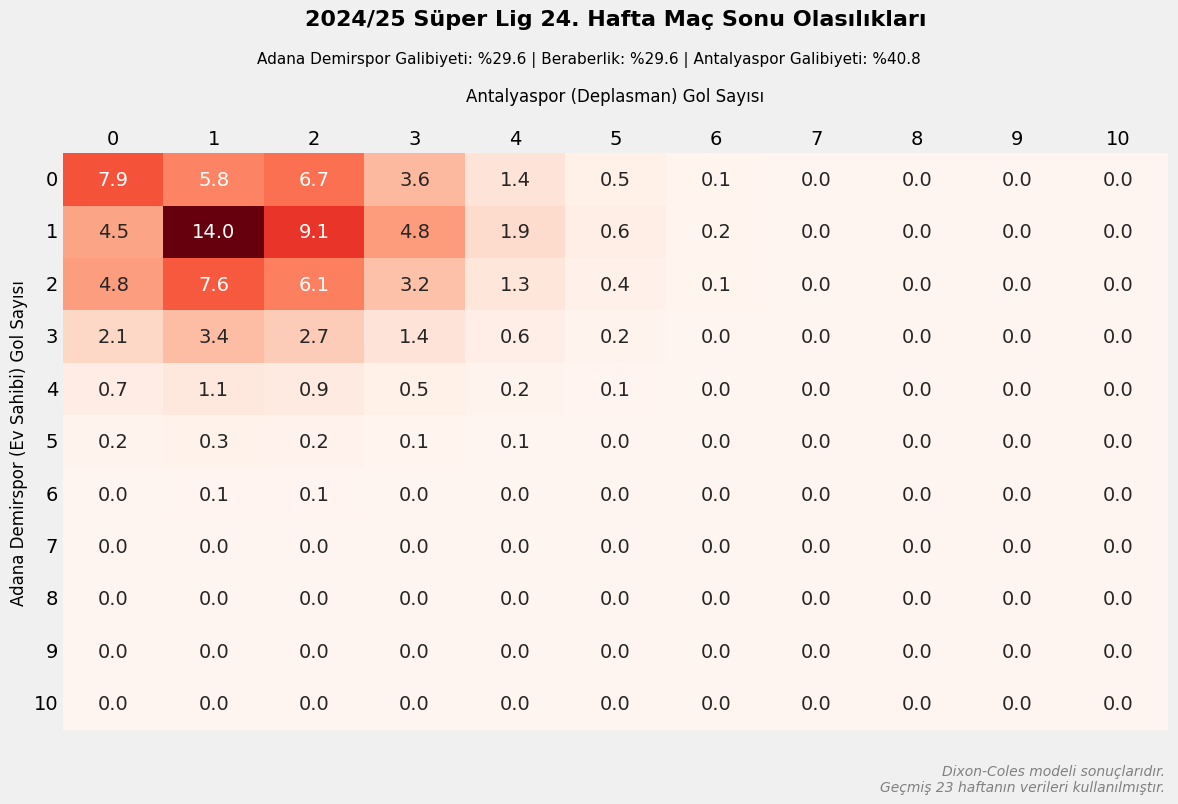

Sonuç

Dixon-Coles modeli, futbol maçı sonuçlarını tahmin etmek için güçlü bir istatistiksel araçtır. Bu model, takımların hücum ve savunma güçlerini, ev sahibi avantajını ve maçlar arasındaki bağımlılığı dikkate alarak daha doğru tahminler yapmayı mümkün kılar.

Bu blog yazısında, modelin teorik temellerini detaylı bir şekilde inceledik ve Python ile nasıl uygulanabileceğini adım adım gösterdik. Dixon-Coles modelini anlamak ve uygulamak isteyenler için faydalı olmasını dilerim.

Sevgiler.